GNSS high-precision positioning principle and RTK technology

- Background
At present, the most widely used positioning method in the surveying and mapping industry is GNSS positioning. The conventional civil GNSS positioning accuracy is about 5-10 meters, which cannot meet the application of high-precision. So how is the centimeter-level positioning used in the surveying and mapping industry? Today we will take you through the GNSS positioning principle and introduce how to realize centimeter-level height positioning.
- The GNSS Localization Principle
- The Basic Concept of GNSS
The Global Navigation Satellite System (GNSS) is a global navigation system based on satellites that provides time/space references and all real-time dynamic information related to positional information. GNSS consists of different satellite systems in many countries, including the U.S. GPS system, the EU Galileo system, the Russian GLONASS system, the Chinese Beidou system, and other regional positioning systems, such as Japanese QZSS, etc.
Figure 1. The four major satellite systems
2.GNSS Positioning Concepts
The basic principle of GNSS positioning is based on ranging the high-precision distance between satellites and GNSS receiver. When the location of satellites is known, the position of GNSS receiver could be obtained.
What information can we use to calculate the distance between the satellite and the GNSS receiver? The receiver can generally obtain two types of distance information.
One is Pseudo-Range, and the other is Carrier Phase-Range.
Pseudo-Range: the moment when the satellite transmitting signal is known. By recording the time when GNSS receiver receives the satellite emission signal, the time when the signal propagation in space can be obtained. Because the signal propagation speed is the speed of light, the distance obtained by multiplying the time difference is called pseudo distance, that is, PR is not the real distance, there is a certain error.
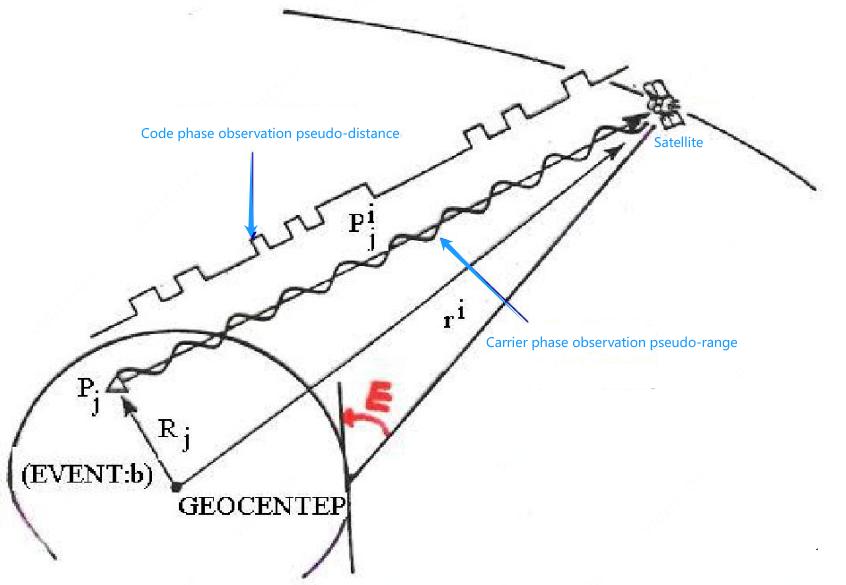
Figure 2. Pseudo-Range
Carrier Phase-Range: It is the use of the periodic phase of an electromagnetic wave to complete the measurement. Because the GNSS signal is an electromagnetic wave, its phase is periodic, so the real phase should be N whole cycles plus an non-cycle phase. The non-week art can be accurately obtained through the phase locking ring, and the whole cycles part N is uncertain, and needs to be determined by other means. That is, Cp = (N + γ) * λ, where N is the whole cycles, γ is the generally unknown non-cycles part, λ is the signal wave length.
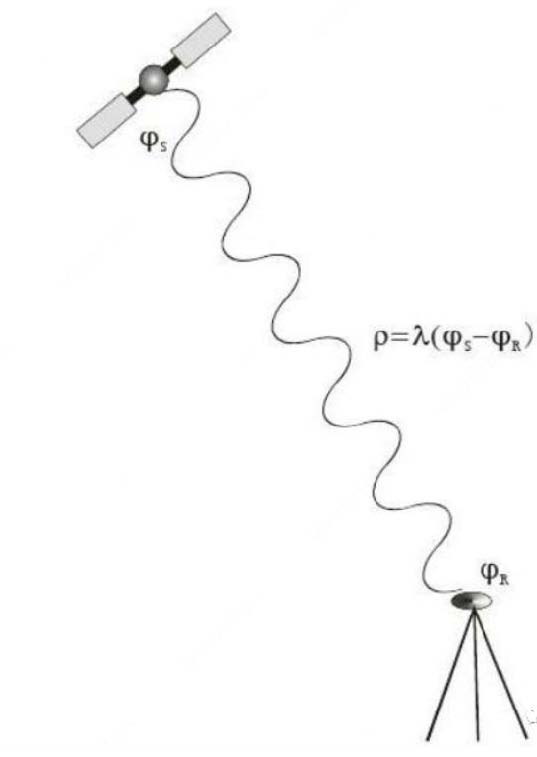
Figure 3. Carrier Phase Range
The main difference between Carrier phase Range and Pseudo-Range is their accuracy. The precision of pseudo distance is generally ~1m. When the ambiguity of the carrier phase is fixed correctly throughout the cycle, the accuracy is ~0.001m. Therefore, based on the pseudo-distance positioning accuracy is generally meter level, according to the carrier phase range degree can be up to cm level.
When we already have the distance between the satellite and the receiver, combined with the ephemeris information, we get the satellite in each moment of the position and speed, combined with the position of the satellite and the distance between the satellite and the receiver, the position of the receiver can be further determined by the least squares method or by the extended Kalman filter.
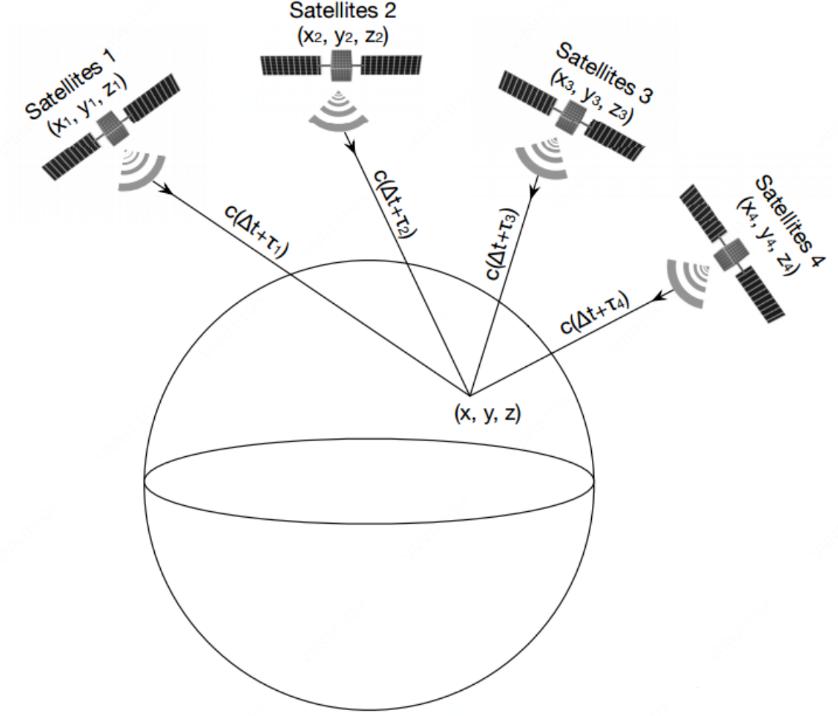
Figure 4. GNSS Localization Basic Principle
- Difficulty with GNSS positioning
In principle, it seems that GNSS positioning is very simple, but is it?
We can take a look at the error sources of it.
1)The GNSS clock is out of sync with the receiver;
2)The clock is not synchronized between different GNSS;
3) The receiver clock generally has drift;
4)In the process of transmission, satellite signals will pass through the atmosphere and troposphere, and there is signal reflection and refraction, so the actual distance or phase is not the true distance;
5)There may be a multipath effect between the receiver and the satellite, resulting in the received signal not being a direct signal;
6)In many places, we can only receive a very small number of satellites and can not meet the positioning needs.
Only some sources of error are listed above, and the reality may be more complicated.
The sources of errors are categorized as follows.
Errors related to satellites: satellite orbit error, satellite clock error.
Errors related to the transmission: ionospheric delay, tropospheric delay, multipath effect.
Errors related to receiving equipment: receiver antenna phase center shifts and variations,
receiver clock errors, etc.
The following figure lists each error source in a schematic way.
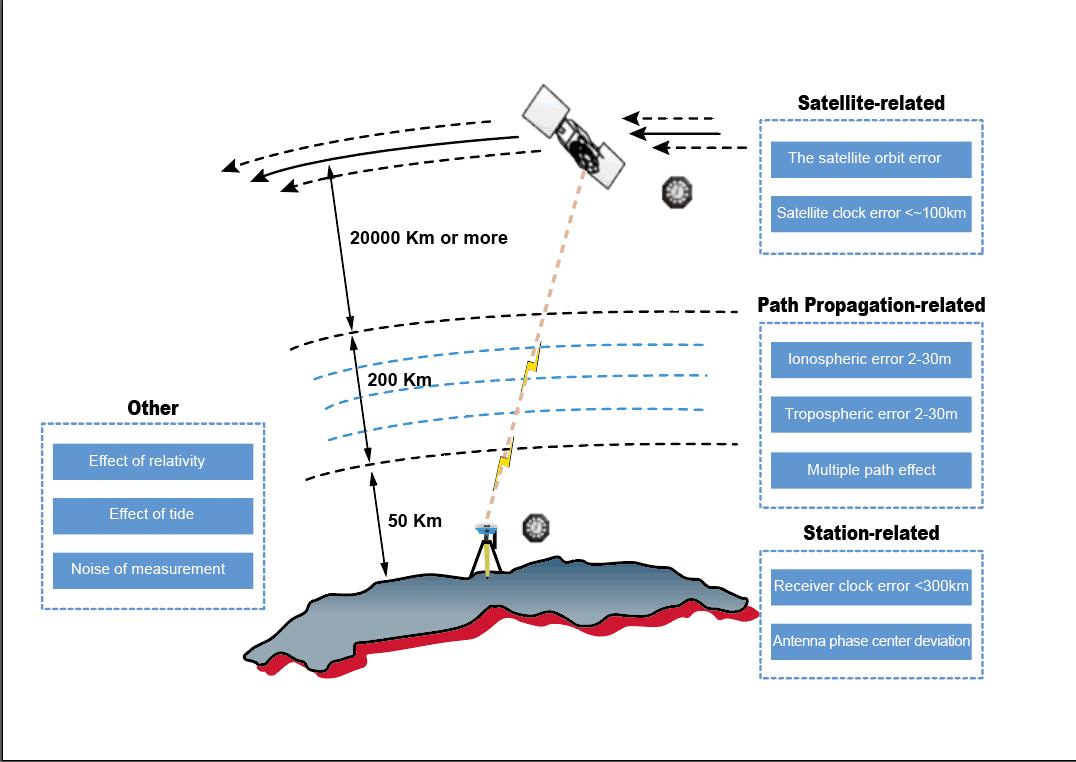
Figure 5. The Range Error during the Propagation Process
- GNSS Positioning Error Elimination Method
There are generally two ways to eliminate the above errors.
1)Model correction method: model the error, estimate its range and compensate.
2)Difference method: eliminate or attenuate the specific error, through the difference. Depending on how to eliminate these error sources, real-time GNSS positioning can be simply divided into single point positioning and RTK positioning.
Single point positioning is directly completed according to the measured pseudo-distance information. In the process of positioning, the receiver clock difference is modeled, and some algorithms will model the ionosphere and troposphere. In the calculation, the broadcast ephemeris has low accuracy, and the final positioning accuracy is generally meter level.
PPP is a precise point positioning, using the precision ephemeris and the receiver and satellite clock difference, clock drift, ionosphere, the troposphere modeling, so as to achieve high precision positioning. PPP positioning accuracy can reach 10cm, but generally slower convergence time, need more than 30min.
RTK is real-time dynamic positioning, and we call the receiver for which we need high-precision positioning information a mobile station. When positioning with RTK, we also need a high-precision receiver whose position information is known, which we call a base station. After the base station receives the GNSS signal, it transmits data to the mobile station through the network or radio station. The mobile station can distinguish the signal received by itself with the information received by the difference station by completely eliminating the parameters such as the clock difference and satellite orbit, and also weaken the influence of the ionosphere and the troposphere.
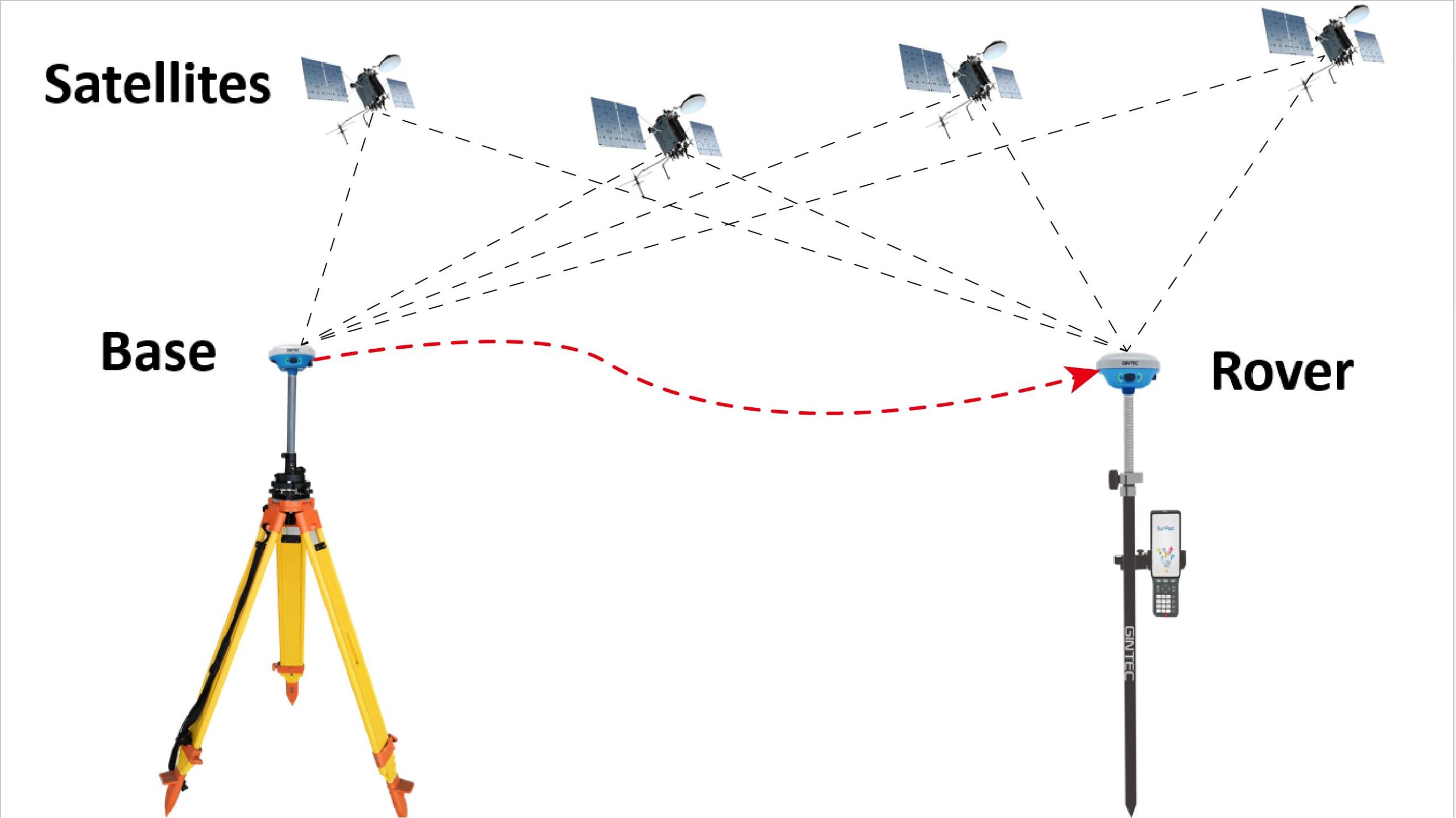
Figure 6. Schematic representation of differential localization
- The Basic Principles of RTK Algorithm
RTK algorithm is the most commonly used GNSS altitude positioning technique, with centimeter-level positioning in open spaces and in a matter of seconds.
In the last time, we introduced the correction of the measurement error, after which we can use the corrected distance to calculate the positioning result. High-precision positioning must be located by carrier phase, but the carrier phase has the whole cycles of ambiguity problem, that is, the fuzzy degree of the whole cycles must be accurately known to obtain accurate positioning results, so the core of RTK algorithm is the whole cycles of ambiguity fixed.
Theoretically, the whole cycles ambiguity N must be an integer, but we estimate according to the least squares method or Kalman filter N is not an integer, but a real number. How do we get an integer according to the real number? The most basic method is to search for all integers around the real number N, and to evaluate the combination of the integers with the smallest selection error as the true whole cycles N. Due to the carrier phase and pseudo distance in the measurement information, the two-measurement accuracy varies greatly, resulting in a huge fuzzy search space and high complexity in the whole cycles. Therefore, we can eliminate the correlation between various parameters through data conversion and narrow the search space, so as to improve the efficiency of the algorithm. Common methods include lambda. As shown in the figure below, the search space decreased significantly before and after the parameter transformation.
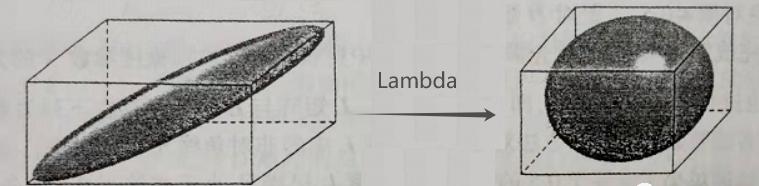
Figure 7. Comparison of search space before and after parameter space transformation
IIII. The Future Trends of RTK Algorithm
We can get high-precision position info by RTK tech in relatively open environments to meet most requirements, but there is still a lot of room for improvement in the future. technology of RTK in complex environments, such as under dense trees, beside large buildings, due to the impact of zenith vision, the positioning accuracy cannot be guaranteed, and therefore cannot rely on RTK alone to complete the high-precision measurement. However, RTK is fast and convenient to use, which significantly improves the efficiency of the traditional surveying and mapping industry. It has become the first choice in many positioning requirements.
At present, as a Trading company specializing in high-accuracy surveying, We focuses on improving and optimizing the applications and accuracy of RTK technology. We have spent much effort and time on it. In the algorithm, we are using a large number of simulation tests in a variety of complex environments, and then optimizing the RTK algorithm of test data through the analysis of the solution speed and positioning accuracy. In addition, we are trying to use more sensor combination ways, such as IMU Sensor, Camera, Laser Range Finder, Bluetooth, WIFI, NFC, and other multiple sensor combination navigation ways, to gradually improve the use of RTK positioning in multi-scenario. We believe that soon we will deliver a good report to the people!
In the next episode, we will introduce another common GNSS positioning: PPP (Precise Point Positioning). Will this technology become the next popular mapping method? So, stay tuned!

